Board Identification
If we have rectangular boards we use the simple identification string "files times ranks". Example: "8x8" is the identification string of the FIDE chess board.
If we have boards with unususal shapes, then we need an extended identification string, which allows to reconstruct the board, and additionally it must allow to compute the squares not belonging to the board. In this way the piece definitions (see MBN) must not take care about the squares not belonging to the board.
With non-rectangular shapes we embed the board inside the smallest rectangle, that is entirely enclosing the board. We use the dimension ("files times rank") of this enclosing rectangle. Then we have to append a computed path. This method has the advantage that it gives quite short strings, and a quite good visual recognition.
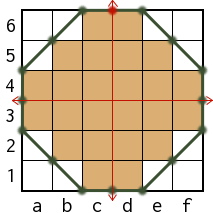
See the examples below. A white square does not belong to the board. The path is visualized as a green line, going from egde cell to egde cell (green point) in clockwise direction. An edge cell is a cell that don't has four cells as neighbors in orthogonal direction (we do not consider holes inside the board). Start point is the red circle (topmost cell at vertical bisector). We want to keep symmetries, so the construction depends on the number of cells, whether we have an even number or an odd number. With an odd number we will use the middle, with an even number we will use the outer edge, the examples below will demonstrate this. We are going edge cell by edge cell, either left, right, down, up, left-down, left-up, right-down, or right-up (but only one cell).
 |
 |
 |
 |
We will build the path for the leftmost example. The start point is the top-right corner of cell C6. We will go from top-right corner to top-right corner, along the green path. So we are going now to cell D6: one cell right, written as (+1,0). The next visited cell is E5: one cell right, and one cell down, this is (+1,-1). The path will be build according to the following table (note that the signs are important and cannot be omitted):
| (+1,+1) | 1 cell right, and 1 cell up |
| (+1,-1) | 1 cell right, and 1 cell down |
| (-1,+1) | 1 cell left, and 1 cell down |
| (-1,-1) | 1 cell left, and 1 cell up |
| (+1,0) | 1 cell right |
| (-1,0) | 1 cell left |
| (0,+1) | 1 cell up |
| (0,-1) | 1 cell down |
After going further in our path we will reach F3. This point is crossing a bisector, so we append a hash marker (#) behind our last move. Then we go to cell F2, denoted as (0,-1). The intermediate path so far is:
After going further we will reach B6 (top-right corner). Here we have to close the path with (+1,0)#, we are back at start cell C6. A hash marker has been added because we have reached the bisector. Every time when crossing a bisector we have to append a hash sign. Finally we get this path:
This will be called an integral path. Now we will perform some bijective operations on the path.
Note that the hash markers are dividing the path into four parts. At first we try to detect point reflection. Reflect all elements in third and fourth part at X and Y axes (flip the x and y components). This is the result:
If now first part is equal to third part, and second part is equal to fourth part, then replace first hash marker (after first part) with a star (*). Then take back the reflections in third and fourth part. We get this result:
Next step is the detection of orthogonal symmetry. We compare the first part (north-east) with second part (south-east), and third part (south-west) with fourth part (north-west). But for comparison we have to reverse the order of elements in second and fourth part. Futhermore we need a reflection at vertical bisector in all elements of second and fourth part (flip the x components). In our example we get:
The first and second part are equal, in this case we will replace the hash marker after second component (here the second hash marker in path) with an equal sign (marker for vertical symmetry).
The same will be applied to third and fourth part: if they are equal, then replace the hash after fourth part with an equal sign. Then take back the reflection in the second and fourth part, our new result is:
Note that the order of the elements in second and third part is still reversed.
For the next step we will do a reflection at horizontal bisector in third and fourth part (flip the y components), the result is:
In our example the first part is equal to fourth part, in this case replace the hash after first part with a colon (marker for horizontal symmetry). In our example we can't do this, because we have a star after first part, but not a hash marker.
If the second part is equal to the third part, then replace the hash after third part with a colon. Next we have to take back the reflection at horizontal bisector in third and fourth part, and we have to take back the reversal of elements in second and fourth part. The result in our example is:We have finished the detection of reflections. Now change the path according to one of the following rules. A denotes the first part, B the second, C the third, and D the fourth. The question mark is matching any marker (minus, colon, star, or hash). The first rule that matches has to be applied. It is very likely that one of the first three pattern will match.
| A*B=C:D= ↦ A= | full symmetry |
| A:B=C:D= ↦ A= | full symmetry |
| A*B?C?D? ↦ AB* | point symmetry |
| A:B#C:D# ↦ AB: | vertical symmetry |
| A#B=C#D= ↦ A=C= | horizontal symmetry |
| A?B?C?D? ↦ ABCD | asymmetry |
In our example we have the result:
The elements will be shortened, according to the following substitutions:
|
|
After a closer look you might see that this mapping scheme is relatively easy to remember.
The result after replacement is:
The next step is to condense all repetitions, by writing a repetition count after the first element, and removing the succeeding repeating elements. Note that we never use repetition count 1. In our example the result is:
Lastly we remove all parentheses:
We only examined the integral path, but the board identification string also contains the dimension of the enclosing rectangle, so our full identification string is:
Finally we have a quite short board identification string.
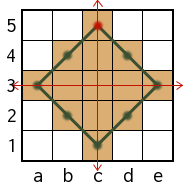
A practical hint: in general the boards are symmetrical in both directions, so it's sufficient to build the path only for the north-east quarter of the board, and then simply append an equal sign.
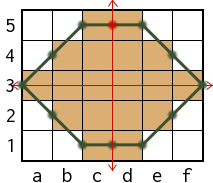
For clarity and completeness we will examine a special case. For simplicity we use a rectangle as example.

The path starts at C1, and is going with (+1,0)(+1,0) to E1, then it goes with #(-1,0)(-1,0)#(-1,0)(-1,0) to A1. We have reached the vertical bisector after the fourth element, thus the second hash marker has been inserted. But note that changing the direction horizontally at horizontal bisector is also inserting a hash (it's like crossing the bisector), thus the first hash marker has been inserted. The same applies when changing the direction vertically at vertical bisector (not the case in our example). Now go back to start point with #(+1,0)(+1,0)#; again we changed the direction horizontally at horizontal bisector (third hash), and finally we reached the vertical bisector (fourth hash). The integral path is:
After doing all the conversions the final identification string is:
Note that identification strings of the following forms are not allowed:
These are rectangles, and this has to be written shortly as ΣxΣ or Σ1xΣ2, respectively. Moreover the path is not needed for rectangular boards.
TODO: proof that the identification string is unambiguous:
- show that each conversion step is bijective
- then simply show that the integral path is unambiguous.
3D boards
Simply prepend the number of levels (boards), followed by an x sign. Example for a variant with 3 levels, and a standard board:
4D boards
In 4D chess we prepend both dimensions. Example for a variant with 4 columns, 4 rows, and a standard board:
Note that the number of columns (3rd dimension) comes first, then the number of rows (4th dimension), but normally a hypercube will be used (i.e. same number of columns and rows).